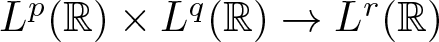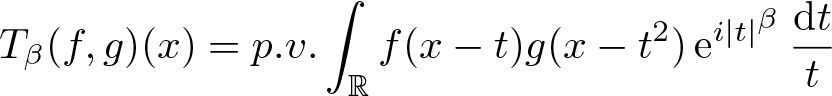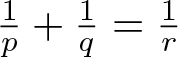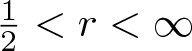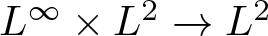1 results
The boundedness of the bilinear oscillatory integral along a parabola
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 54-88
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, the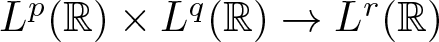
$L^p(\mathbb{R})\times L^q(\mathbb{R})\rightarrow L^r(\mathbb{R})$ boundedness of the bilinear oscillatory integral along parabolais set up, where β > 1 or β < 0,
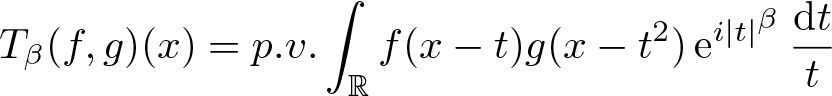\begin{equation*}T_\beta(f, g)(x)=p.v.\int_{{\mathbb R}} f(x-t)g(x-t^{2})\,{\rm e}^{i |t|^{\beta}}\,\frac{{\rm d}t}{t}\end{equation*}
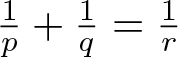$\frac{1}{p}+\frac{1}{q}=\frac{1}{r}$ and 
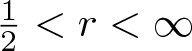$\frac{1}{2}\lt r\lt\infty$, p > 1 and q > 1. The result for the case β < 0 extends the 
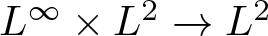$L^\infty\times L^2\to L^2$ boundedness obtained by Fan and Li (D. Fan and X. Li, A bilinear oscillatory integral along parabolas, Positivity 13(2) (2009), 339–366) by confirming an open question raised in it.
