We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that bounded John domains and bounded starshaped domains with respect to a point satisfy the following inequality
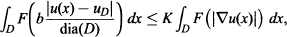
where F: [0, ∞) → [0, ∞) is a continuous, convex function with F(0) = 0, and u is a function from an appropriate Sobolev class. Constants b and K do depend at most on D. If F(x) = xp, 1 ≤ p < ∞, this inequality reduces to the ordinary Poincaré inequality.
