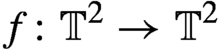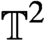1 results
Flexibility of Lyapunov exponents with respect to two classes of measures on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 737-776
- Print publication:
- February 2022
-
- Article
- Export citation
-
We consider a smooth area-preserving Anosov diffeomorphism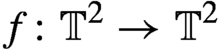
$f\colon \mathbb T^2\rightarrow \mathbb T^2$
homotopic to an Anosov automorphism L of 
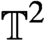$\mathbb T^2$
. It is known that the positive Lyapunov exponent of f with respect to the normalized Lebesgue measure is less than or equal to the topological entropy of L, which, in addition, is less than or equal to the Lyapunov exponent of f with respect to the probability measure of maximal entropy. Moreover, the equalities only occur simultaneously. We show that these are the only restrictions on these two dynamical invariants.
