We give a motivic proof of the fact that for nonsingular real tropical complete intersections, the Euler characteristic of the real part is equal to the signature of the complex part. This was originally proved by Itenberg in the case of surfaces in 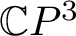$\mathbb {C}P^{3}$, and has been successively generalized by Bertrand and by Bihan and Bertrand. Our proof, different from previous approaches, is an application of the motivic nearby fiber of semistable degenerations. In particular, it extends the original result by Itenberg, Bertrand, and Bihan to real analytic families admitting a 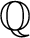$\mathbb {Q}$-nonsingular tropical limit.

We globalize the derived version of the McKay correspondence of Bridgeland, King and Reid, proven by Kawamata in the case of abelian quotient singularities, to certain logarithmic algebraic stacks with locally free log structure. The two sides of the correspondence are given respectively by the infinite root stack and by a certain version of the valuativization (the projective limit of every possible logarithmic blow-up). Our results imply, in particular, that in good cases the category of coherent parabolic sheaves with rational weights is invariant under logarithmic blow-up, up to Morita equivalence.