We prove the existence of positive radial solutions to a class of semipositone p-Laplacian problems on the exterior of a ball subject to Dirichlet and nonlinear boundary conditions. Using variational methods we prove the existence of a solution, and then use a priori estimates to prove the positivity of the solution.

We investigate the stability properties of positive steady-state solutions of semilinear initial–boundary-value problems with nonlinear boundary conditions. In particular, we employ a principle of linearized stability for this class of problems to prove sufficient conditions for the stability and instability of such solutions. These results shed some light on the combined effects of the reaction term and the boundary nonlinearity on stability properties. We also discuss various examples satisfying our hypotheses for stability results in dimension 1. In particular, we provide complete bifurcation curves for positive solutions for these examples.

We consider a quasilinear elliptic problem of the form

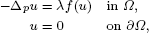
where λ > 0 is a parameter, 1 < p < 2 and Ω is a strictly convex bounded domain in ℝN, N > p, with C2 boundary ∂Ω. The nonlinearity f : [0, ∞) → ℝ is a continuous function that is semipositone (f(0) < 0) and p-superlinear at infinity. Using degree theory, combined with a rescaling argument and uniform L∞a priori bound, we establish the existence of a positive solution for λ small. Moreover, we show that there exists a connected component of positive solutions bifurcating from infinity at λ = 0. We also extend our study to systems.