We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A Latin square is reduced if its first row and first column are in natural order. For Latin squares of a particular order 
$n$, there are four possible different parities. We confirm a conjecture of Stones and Wanless by showing asymptotic equality between the numbers of reduced Latin squares of each possible parity as the order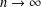 
$n\rightarrow \infty$.
