We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We classify the automorphic Lie algebras of equivariant maps from a complex torus to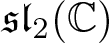 
$\mathfrak{sl}_2(\mathbb{C})$. For each case, we compute a basis in a normal form. The automorphic Lie algebras correspond precisely to two disjoint families of Lie algebras parametrised by the modular curve of 
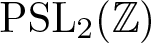$\mathrm{PSL}_2({\mathbb{Z}})$, apart from four cases, which are all isomorphic to Onsager’s algebra.
