Let X be a d-dimensional continuous super-Brownian motion with branching rate ε, which might be described symbolically by the "stochastic equation" 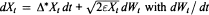 a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of X on path space as ε → 0, with a representation of the rate functional via an L2 -functional on a generalized "Cameron-Martin space" of measure-valued paths.
a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of X on path space as ε → 0, with a representation of the rate functional via an L2 -functional on a generalized "Cameron-Martin space" of measure-valued paths.