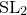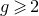1 results
On quasimap invariants of moduli spaces of Higgs bundles
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We compute odd-degree genus 1 quasimap and Gromov–Witten invariants of moduli spaces of Higgs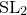
${\rm{S}}{{\rm{L}}_2}$-bundles on a curve of genus 
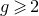$g \geqslant 2$. We also compute certain invariants for all prime ranks. This proves some parts of the author’s conjectures on quasimap invariants of moduli spaces of Higgs bundles. More generally, our methods provide a computation scheme for genus 1 quasimap and Gromov–Witten invariants in the case when degrees of maps are coprime to the rank. This requires an analysis of the localisation formula for certain Quot schemes parametrising higher-rank quotients on an elliptic curve. Invariants for degrees that are not coprime to the rank exhibit a very different structure for a reason that we explain.
