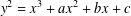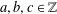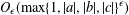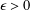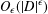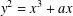1 results
A NOTE ON SCHMIDT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 09 June 2017, pp. 191-195
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
-
Schmidt [‘Integer points on curves of genus 1’, Compos. Math. 81 (1992), 33–59] conjectured that the number of integer points on the elliptic curve defined by the equation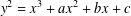
$y^{2}=x^{3}+ax^{2}+bx+c$, with 
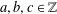$a,b,c\in \mathbb{Z}$, is 
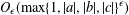$O_{\unicode[STIX]{x1D716}}(\max \{1,|a|,|b|,|c|\}^{\unicode[STIX]{x1D716}})$ for any 
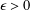$\unicode[STIX]{x1D716}>0$. On the other hand, Duke [‘Bounds for arithmetic multiplicities’, Proc. Int. Congress Mathematicians, Vol. II (1998), 163–172] conjectured that the number of algebraic number fields of given degree and discriminant 
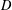$D$ is 
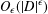$O_{\unicode[STIX]{x1D716}}(|D|^{\unicode[STIX]{x1D716}})$. In this note, we prove that Duke’s conjecture for quartic number fields implies Schmidt’s conjecture. We also give a short unconditional proof of Schmidt’s conjecture for the elliptic curve 
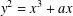$y^{2}=x^{3}+ax$.
