We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We shall define a general notion of dimension, and study groups and rings whose interpretable sets carry such a dimension. In particular, we deduce chain conditions for groups, definability results for fields and domains, and show that a pseudofinite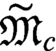 
$\widetilde {\mathfrak M}_c$
-group of finite positive dimension contains a finite-by-abelian subgroup of positive dimension, and a pseudofinite group of dimension 2 contains a soluble subgroup of dimension 2.
