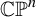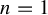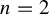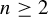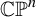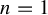A holomorphic endomorphism of ${{\mathbb {CP}}}^n$ is post-critically algebraic if its critical hypersurfaces are periodic or preperiodic. This notion generalizes the notion of post-critically finite rational maps in dimension one. We will study the eigenvalues of the differential of such a map along a periodic cycle. When $n=1$ , a well-known fact is that the eigenvalue along a periodic cycle of a post-critically finite rational map is either superattracting or repelling. We prove that, when 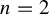$n=2$ , the eigenvalues are still either superattracting or repelling. This is an improvement of a result by Mattias Jonsson [Some properties of 2-critically finite holomorphic maps of P2. Ergod. Th. & Dynam. Sys.18(1) (1998), 171–187]. 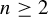When $n\geq 2$ and the cycle is outside the post-critical set, we prove that the eigenvalues are repelling. This result improves one obtained by Fornæss and Sibony [Complex dynamics in higher dimension. II. Modern Methods in Complex Analysis (Princeton, NJ, 1992) (Annals of Mathematics Studies, 137). Ed. T. Bloom, D. W. Catlin, J. P. D’Angelo and Y.-T. Siu, Princeton University Press, 1995, pp. 135–182] under a hyperbolicity assumption on the complement of the post-critical set.