1 results
T-convexity and tame extensions
-
- Journal:
- The Journal of Symbolic Logic / Volume 60 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 March 2014, pp. 74-102
- Print publication:
- March 1995
-
- Article
- Export citation
-
Let T be a complete o-minimal extension of the theory of real closed fields. We characterize the convex hulls of elementary substructures of models of T and show that the residue field of such a convex hull has a natural expansion to a model of T. We give a quantifier elimination relative to T for the theory of pairs (ℛ, V) where ℛ ⊨ T and V ≠ ℛ is the convex hull of an elementary substructure of ℛ. We deduce that the theory of such pairs is complete and weakly o-minimal. We also give a quantifier elimination relative to T for the theory of pairs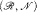
with ℛ a model of T and 
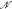a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.
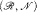with ℛ a model of 
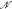a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.