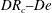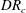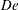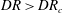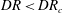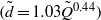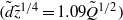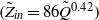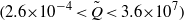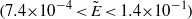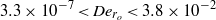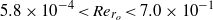The stability of fibre spinning flow of a polymeric fluid is analysed in the presence of thermal effects. The spinline is modelled as a one-dimensional slender-body filament of the entangled polymer solution. The previous study (Gupta & Chokshi, J. Fluid Mech., vol. 776, 2015, pp. 268–289) analysed linear and nonlinear stability behaviour of an isothermal extensional flow in the air gap during the fibre spinning process. The present study extends the analysis to take in to account the non-isothermal spinning flow in which the spinline loses heat by convection to the surrounding air as well as by solvent evaporation. The nonlinear rheology of the polymer solution is described using the eXtended Pom-Pom (XPP) model. The non-isothermal effects influence the rheology of the fluid through viscosity, which is taken to be temperature and concentration dependent. The linear stability analysis is carried out to obtain the draw ratio for the onset of instability, known as the draw resonance, and a stability diagram is constructed in the $DR_{c}{-}De$ plane. $DR_{c}$ is the critical draw ratio, and $De$ is the flow Deborah number. The enhancement in viscosity driven by spinline cooling leads to postponement in the onset of draw resonance, indicating the stabilising role of non-isothermal effects. Weakly nonlinear stability analysis is also performed to reveal the role of nonlinearities in the finite amplitude manifold in the vicinity of the flow transition point. For low to moderate Deborah numbers, the bifurcation is supercritical, and the flow attains an oscillatory state with an equilibrium amplitude post-transition when $DR>DR_{c}$. The equilibrium amplitude of the resonating state is found to be smaller when non-isothermal effects are incorporated in comparison to the isothermal spinning flow. For very fast flows in the regime of high Deborah numbers, the finite amplitude manifold crosses over to a subcritical state. In this limit, the nonlinearities render the flow unstable even in the linearly stable regime of $DR<DR_{c}$.

Polymer-containing solutions used across research and industry are commonly exposed to mechanically harsh fluid processes, for example shear and extensional forces during flow through porous media or rapid microdispensing of biopharmaceutical molecules. These forces are strong enough to break the covalent bonds in the polymer backbone. As this scission phenomenon can change the functional and fluid-flow properties as well as introduce reactive radicals into the solution, it must be understood and controlled. Experiments and models to date have only provided partial or qualitative insights into this behaviour. Here we build a link between the molecular-scale degradation models and the macroscale laminar flow of dilute solutions in any given geometry. A free-draining bead–rod model is used to investigate rupture events at the molecular scale. It is shown by uniaxial extension simulations of an ensemble of chains that scission can be conveniently described at the macroscopic scale as a first-order reaction whose rate is a function of the conformation tensor of the macromolecules and the velocity gradient of the flow. This approach is implemented in the finite volume code OpenFOAM by elaborating an appropriate constitutive equation for the conformation tensor. The macroscopic model is run and analysed for ultra-dilute solutions of poly(methyl methacrylate) in ethyl acetate and polyethylene oxide in water, using the geometry of an abrupt contraction flow and neglecting any viscoelastic effect. This multiscale approach bridges the gap between phenomenological observations of mechanically induced chemical degradation in large-scale applications and the rich field of molecular-scale models of macromolecules under flow.

An electrospun polymer jet issued from a Taylor cone follows a straight-line motion before experiencing electrical bending instability resulting in curling and spiralling of the jet in three-dimensional space. Experiments are performed to characterize the fluid dynamics of an electrospun polymer jet. Appropriate image processing is performed to systematically analyse flow regimes of the electrospun jet. These regimes include Taylor cone formation/jet initiation and the straight section of the jet. Dimensional analysis was performed to identify the salient dimensionless parameters, which govern the electrospun jet characteristics. Three new correlation formulae were obtained to characterize the dimensionless jet diameter at the apex of the Taylor cone $(\tilde {d} = 1. 03{\tilde {Q} }^{0. 44} )$, the dimensionless jet diameter at different locations along the jet’s straight section $(\tilde {d} {\tilde {z} }^{1/ 4} = 1. 09{\tilde {Q} }^{1/ 2} )$, as well as the length of the straight section of the jet $({\tilde {Z} }_{in} = 86{\tilde {Q} }^{0. 42} )$. These correlation formulae are valid for the analysed range of dimensionless flow rates $(2. 6{{\times 10}}^{- 4} \lt \tilde {Q} \lt 3. 6{{\times 10}}^{7} )$ and dimensionless electric fields $(7. 4{{\times 10}}^{- 4} \lt \tilde {E} \lt 1. 4{{\times 10}}^{- 1} )$. In addition, the correlation formulae are valid for the analysed range of Deborah numbers De and Reynolds numbers Re based on nozzle radius, $3. 3\times {10}^{- 7} \lt {\mathit{De}}_{{r}_{o} } \lt 3. 8\times {10}^{- 2} $ and $5. 8\times {10}^{- 4} \lt {\mathit{Re}}_{{r}_{o} } \lt 7. 0\times {10}^{- 1} $. The proposed new correlation formulae are instrumental in the design as well as controlled manipulation/optimization of the electrospinning phenomenon.

This paper presents an exact formula for calculating the fourth-moment tensor from the second-moment tensor for the three-dimensional Jeffery's equation. Although this approach falls within the category of a moment tensor closure, it does not rely upon an approximation, either analytic or curve fit, of the fourth-moment tensor as do previous closures. This closure is orthotropic in the sense of Cintra & Tucker (J. Rheol., vol. 39, 1995, p. 1095), or equivalently, a natural closure in the sense of Verleye & Dupret (Developments in Non-Newtonian Flow, 1993, p. 139). The existence of these explicit formulae has been asserted previously, but as far as the authors know, the explicit forms have yet to be published. The formulae involve elliptic integrals, and are valid whenever fibre orientation was isotropic at some point in time. Finally, this paper presents the fast exact closure, a fast and in principle exact method for solving Jeffery's equation, which does not require approximate closures nor the elliptic integral computation.

Le comportement d'un polypropylène chargé de fibres de verre courtes a été étudié. À l'état fondu, un thermoplastique renforcé de fibres courtes ayant un état d'orientation initial isotrope présente un pic de viscosité lorsqu'il est cisaillé entre les deux disques d'un rhéomètre à géométrie plan–plan. Dans cette étude, après une première déformation, l'échantillon a été cisaillé dans la direction inverse et un pic de viscosité a été à nouveau mesuré. De même des pics de contraintes normales ont été observés. Dans l'écoulement inverse les contraintes normales passent par des valeurs négatives puis présentent un pic positif. Un modèle a été utilisé pour simuler ces pics de viscosité et de contraintes normales. Il est constitué de l'équation de Folgar-Tucker pour le mouvement des fibres et de l'équation de Lipscomb pour la loi de comportement. Ces équations ont été établies pour des solutions diluées ou semi-diluées de fibres. Ces composites industriels sont considérés comme des suspensions concentrées, les fibres sont proches de leurs voisines et leurs rotations sont plus lentes que ce que prédit la simulation. Ce modèle a été empiriquement modifié pour simuler correctement les pics lorsque le taux de fibre augmente.