1 results
SOME WEAKER FORMS OF THE CHAIN (F) CONDITION FOR METACOMPACTNESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 283-288
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
-
We define, in a slightly unusual way, the rank of a partially ordered set. Then we prove that if X is a topological space and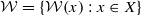
satisfies condition (F) and, for every x∈X, 
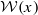is of the form 
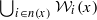, where 
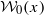is Noetherian of finite rank, and every other 
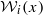is a chain (with respect to inclusion) of neighbourhoods of x, then X is metacompact. We also obtain a cardinal extension of the above. In addition, we give a new proof of the theorem ‘if the space X has a base 
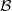of point-finite rank, then X is metacompact’, which was proved by Gruenhage and Nyikos.
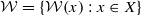satisfies condition (
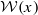is of the form 
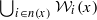, where 
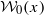is Noetherian of finite rank, and every other 
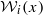is a chain (with respect to inclusion) of neighbourhoods of 
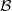of point-finite rank, then 