We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The Bruss–Robertson–Steele (BRS) inequality bounds the expected number of items of random size which can be packed into a given suitcase. Remarkably, no independence assumptions are needed on the random sizes, which points to a simple explanation; the inequality is the integrated form of an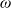 
$\omega$-by-
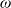$\omega$ inequality, as this note proves.
