In this paper, a reflected stochastic differential equation (SDE) with jumps is studied for the case where the constraint acts on the law of the solution rather than on its paths. These reflected SDEs have been approximated by Briand et al. (2016) using a numerical scheme based on particles systems, when no jumps occur. The main contribution of this paper is to prove the existence and the uniqueness of the solutions to this kind of reflected SDE with jumps and to generalize the results obtained by Briand et al. (2016) to this context.

We consider a strong Markov process with killing and prove an approximation method forthe distribution of the process conditioned not to be killed when it is observed. Themethod is based on a Fleming−Viot type particle system with rebirths, whose particles evolve asindependent copies of the original strong Markov process and jump onto each others insteadof being killed. Our only assumption is that the number of rebirths of theFleming−Viot type systemdoesn’t explode in finite time almost surely and that the survival probability of theoriginal process remains positive in finite time. The approximation method generalizesprevious results and comes with a speed of convergence. A criterion for the non-explosionof the number of rebirths is also provided for general systems of time and environmentdependent diffusion particles. This includes, but is not limited to, the case of theFleming−Viot type system ofthe approximation method. The proof of the non-explosion criterion uses an originalnon-attainability of (0,0)result for pair of non-negative semi-martingales with positive jumps.

We define a class of two-dimensional Markov random graphs with I, V, T and Y-shaped nodes (vertices). These are termed polygonal models. The construction extends our earlier work [1]– [5]. Most of the paper is concerned with consistent polygonal models which are both stationary and isotropic and which admit an alternative description in terms of the trajectories in space and time of a one-dimensional particle system with motion, birth, death and branching. Examples of computer simulations based on this description are given.

We consider a branching Brownian motion on 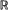starting with n particles of mass 1/n, with interactive branching dynamics. The parameters are unsealed, but depend on the present state of the measure-valued process. For this mean-field model, which is a generalization of Chauvin and Rouault (1990) and Nappo and Orlandi (1988), we prove a propagation of chaos and a fluctuation theorem in 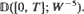([0, T]; W–5).

Particles enter a state space at random times. Each particle travels in the space independent of the other particles until its death. Functionals of the particle system are studied with strong laws and central limit theorems being obtained.