1 results
Hölderian invariance principle for Hilbertian linear processes
-
- Journal:
- ESAIM: Probability and Statistics / Volume 13 / July 2009
- Published online by Cambridge University Press:
- 04 July 2009, pp. 261-275
- Print publication:
- July 2009
-
- Article
- Export citation
-
Let $(\xi_n)_{n\ge 1}$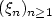
be the polygonal partial sums processes built on the linear processes $X_n=\sum_{i\ge 0}a_i(\epsilon_{n-i})$ 
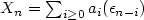, n ≥ 1, where $(\epsilon_i)_{i\in\mathbb{Z}}$ 
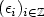are i.i.d., centered random elements in some separable Hilbert space $\mathbb{H}$ 
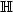and the a i 's are bounded linear operators $\mathbb{H}\to \mathbb{H}$ 
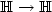, with $\sum_{i\ge 0}\lVert a_i\rVert<\infty$ 
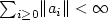. We investigate functional central limit theorem for $\xi_n$ 
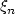in the Hölder spaces $\mathrm{H}^o_\rho(\mathbb{H})$ 
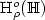of functions $x:[0,1]\to\mathbb{H}$ 
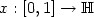such that ||x(t + h) - x(t)|| = o(p(h)) uniformly in t, where p(h) = hαL(1/h), 0 ≤ h ≤ 1 with 0 ≤ α ≤ 1/2 and L slowly varying at infinity. We obtain the $\mathrm{H}^o_\rho(\mathbb{H})$ 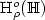weak convergence of $\xi_n$ 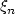to some $\mathbb{H}$ 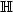valued Brownian motion under the optimal assumption that for any c>0, $tP(\lVert \epsilon_0\rVert>ct^{1/2}\rho(1/t))=o(1)$ 
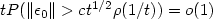when t tends to infinity, subject to some mild restriction on L in the boundary case α = 1/2. Our result holds in particular with the weight functions p(h) = h1/2 lnβ(1/h), β > 1/2>.
