We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider random i.i.d. samples of absolutely continuous measures on bounded connected domains. We prove an upper bound on the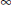 
$\infty $-transportation distance between the measure and the empirical measure of the sample. The bound is optimal in terms of scaling with the number of sample points.
