We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We discuss the concept of inner function in reproducing kernelHilbert spaces with an orthogonal basis of monomials and examine connections between inner functions and optimal polynomial approximants to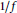 
${1}/{f}\;$, where 
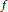$f$ is a function in the space. We revisit some classical examples from this perspective, and show how a construction of Shapiro and Shields can be modiûed to produce inner functions.
