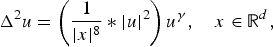2 results
Classification of nonnegative solutions to a bi-harmonic equation with Hartree type nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 979-994
- Print publication:
- August 2019
-
- Article
- Export citation
-
In this paper, we are concerned with the following bi-harmonic equation with Hartree type nonlinearity
where 0 < γ ⩽ 1 and d ⩾ 9. By applying the method of moving planes, we prove that nonnegative classical solutions u to (𝒫γ) are radially symmetric about some point x0 ∈ ℝd and derive the explicit form for u in the Ḣ2 critical case γ = 1. We also prove the non-existence of nontrivial nonnegative classical solutions in the subcritical cases 0 < γ < 1. As a consequence, we also derive the best constants and extremal functions in the corresponding Hardy-Littlewood-Sobolev inequalities.
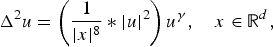$$\Delta ^2u = \left( {\displaystyle{1 \over { \vert x \vert ^8}}* \vert u \vert ^2} \right)u^\gamma ,\quad x\in {\open R}^d,$$
Bifurcation of steady-state solutions of a scalar reaction-diffusion equation in one space variable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-355
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
