We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The Krasnosel’skiĭ–Mann (KM) iteration is a widely used method to solve fixed point problems. This paper investigates the convergence rate for the KM iteration. We first establish a new convergence rate for the KM iteration which improves the known big-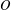
$O$ rate to little-
$o$ without any other restrictions. The proof relies on the connection between the KM iteration and a useful technique on the convergence rate of summable sequences. Then we apply the result to give new results on convergence rates for the proximal point algorithm and the Douglas–Rachford method.
