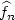1 results
Adaptive density estimation under weak dependence
-
- Journal:
- ESAIM: Probability and Statistics / Volume 14 / 2010
- Published online by Cambridge University Press:
- 10 May 2010, pp. 151-172
- Print publication:
- 2010
-
- Article
- Export citation
-
Assume that (Xt )t∈Z is a real valued time seriesadmitting a common marginal density f with respect to Lebesgue's measure. [Donoho et al. Ann. Stat.24 (1996) 508–539] propose near-minimax estimators $\widehat f_n$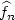
based on thresholding wavelets to estimate f on a compact set in an independent and identically distributed setting. The aim of the present work is to extend these results to general weak dependent contexts. Weak dependence assumptions are expressed as decreasing bounds of covariance terms and are detailed for different examples. The threshold levels in estimators $\widehat f_n$ 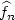depend on weak dependence properties of the sequence (Xt )t∈Z through the constant. If these properties are unknown, we propose cross-validation procedures to get new estimators. These procedures are illustrated via simulations of dynamical systems and non causal infinite moving averages. We also discuss the efficiency of our estimators with respect to the decrease of covariances bounds.
