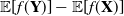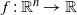For two n-dimensional elliptical random vectors X and Y, we establish an identity for 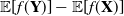$\mathbb{E}[f({\bf Y})]- \mathbb{E}[f({\bf X})]$, where 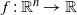$f\,{:}\, \mathbb{R}^n \rightarrow \mathbb{R}$ satisfies some regularity conditions. Using this identity we provide a unified method to derive sufficient and necessary conditions for classifying multivariate elliptical random vectors according to several main integral stochastic orders. As a consequence we obtain new inequalities by applying the method to multivariate elliptical distributions. The results generalize the corresponding ones for multivariate normal random vectors in the literature.

The tail dependence of multivariate distributions is frequently studied via the tool of copulas. In this paper we develop a general method, which is based on multivariate regular variation, to evaluate the tail dependence of heavy-tailed scale mixtures of multivariate distributions, whose copulas are not explicitly accessible. Tractable formulae for tail dependence parameters are derived, and a sufficient condition under which the parameters are monotone with respect to the heavy tail index is obtained. The multivariate elliptical distributions are discussed to illustrate the results.