1 results
Nilsequences and multiple correlations along subsequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 08 October 2018, pp. 1634-1654
- Print publication:
- June 2020
-
- Article
- Export citation
-
The results of Bergelson, Host and Kra, and Leibman state that a multiple polynomial correlation sequence can be decomposed into a sum of a nilsequence (a sequence defined by evaluating a continuous function along an orbit in a nilsystem) and a null sequence (a sequence that goes to zero in density). We refine their results by proving that the null sequence goes to zero in density along polynomials evaluated at primes and along the Hardy sequence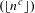
$(\lfloor n^{c}\rfloor )$. In contrast, given a rigid sequence, we construct an example of a correlation whose null sequence does not go to zero in density along that rigid sequence. As a corollary of a lemma in the proof, the formula for the pointwise ergodic average along polynomials of primes in a nilsystem is also obtained.
