1 results
P-hierarchy on βω
-
- Journal:
- The Journal of Symbolic Logic / Volume 73 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1202-1214
- Print publication:
- December 2008
-
- Article
- Export citation
-
We classify ultrafilters on ω with respect to sequential contours (see [4]. [5]) of different ranks. In this way we obtain an ω1 sequence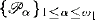
of disjoint classes. We prove that non-emptiness of 
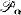for successor α ≥ 2 is equivalent to the existence of P-point. We investigate relations between P-hierarchy and ordinal ultrafilters (introduced by J. E. Baumgartner in [1]). we prove that it is relatively consistent with ZFC that the successor classes (for α ≥ 2) of P-hierarchy and ordinal ultrafilters intersect but are not the same.
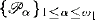of disjoint classes. We prove that non-emptiness of 
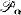for successor 