We present a uniform and easy-to-use technique for deciding the equivalence problem for deterministic monadic linear recursive programs. The key idea is to reduce this problem to the well-known group-theoretic problems by revealing an algebraic nature of program computations. We show that the equivalence problem for monadic linear recursive programs over finite and fixed alphabets of basic functions and logical conditions is decidable in polynomial time for the semantics based on the free monoids and free commutative monoids.

A unified study is undertaken of finitely generated varieties HSP (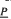) of distributive lattices with unary operations, extending work of Cornish. The generating algebra (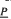) is assusmed to be of the form (P; ∧, ∨, 0, 1, {fμ}), where each fμ is an endomorphism or dual endomorphism of (P; ∧, ∨, 0, 1), and the Priestly dual of this lattice is an ordered semigroup N whose elements act by left multiplication to give the maps dual to the operations fμ. Duality theory is fully developed within this framework, into which fit many varieties arising in algebraic logic. Conditions on N are given for the natural and Priestley dualities for HSP (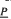) to be essentially the same, so that, inter alia, coproducts in HSP (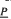) are enriched D-coproducts.