1 results
Riesz-type criteria for L-functions in the Selberg class
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1062-1088
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
We formulate a generalization of Riesz-type criteria in the setting of L-functions belonging to the Selberg class. We obtain a criterion which is sufficient for the grand Riemann hypothesis (GRH) for L-functions satisfying axioms of the Selberg class without imposing the Ramanujan hypothesis on their coefficients. We also construct a subclass of the Selberg class and prove a necessary criterion for GRH for L-functions in this subclass. Identities of Ramanujan–Hardy–Littlewood type are also established in this setting, specific cases of which yield new transformation formulas involving special values of the Meijer G-function of the type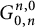
${G^{n , 0}_{0 , n}}$.
