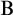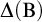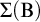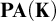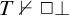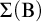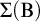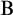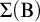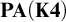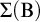1 results
DISJUNCTION AND EXISTENCE PROPERTIES IN MODAL ARITHMETIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 December 2022, pp. 178-205
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
We systematically study several versions of the disjunction and the existence properties in modal arithmetic. First, we newly introduce three classes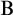
$\mathrm {B}$, 
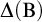$\Delta (\mathrm {B})$, and 
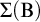$\Sigma (\mathrm {B})$ of formulas of modal arithmetic and study basic properties of them. Then, we prove several implications between the properties. In particular, among other things, we prove that for any consistent recursively enumerable extension T of 
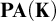$\mathbf {PA}(\mathbf {K})$ with 
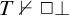$T \nvdash \Box \bot $, the 
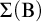$\Sigma (\mathrm {B})$-disjunction property, the 
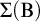$\Sigma (\mathrm {B})$-existence property, and the 
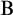$\mathrm {B}$-existence property are pairwise equivalent. Moreover, we introduce the notion of the 
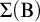$\Sigma (\mathrm {B})$-soundness of theories and prove that for any consistent recursively enumerable extension of 
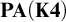$\mathbf {PA}(\mathbf {K4})$, the modal disjunction property is equivalent to the 
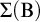$\Sigma (\mathrm {B})$-soundness.
