The joint estimation of both drift and diffusion coefficient parameters is treatedunder the situation where the data are discretely observed from an ergodic diffusion processand where the statistical model may or may not include the true diffusion process.We consider the minimum contrast estimator,which is equivalent to the maximum likelihood type estimator, obtained from the contrast function based on a locally Gaussian approximation of the transition density.The asymptotic normality of the minimum contrast estimator is proved.In particular, the rate of convergence for the minimum contrast estimator of diffusion coefficient parameter in a misspecified modelis different from the one in the correctly specified parametric model.

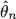 of
of 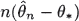 converges in law and in
converges in law and in 