Many statistical applications require establishingcentral limit theorems for sums/integrals $S_T(h)=\int_{t \in I_T} h (X_t) {\rm d}t$ 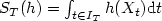or for quadratic forms $Q_T(h)=\int_{t,s \in I_T} \hat{b}(t-s) h (X_t, X_s) {\rm d}s {\rm d}t$ 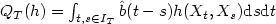, where X t is a stationaryprocess. A particularly important case is that of Appellpolynomials h(X t ) = P m (X t ), h(X t ,X s ) = P m , n (X t ,X s ), since the “Appell expansion rank" determines typically thetype of central limit theorem satisfied by the functionalsS T (h), Q T (h). We review and extend here to multidimensional indices, along lines conjectured in [F. Avram and M.S. Taqqu, Lect. Notes Statist.187 (2006) 259–286], a functionalanalysis approach to this problem proposed by [Avram and Brown, Proc. Amer.Math. Soc.107 (1989) 687–695] based on the method of cumulants and on integrabilityassumptions in the spectral domain; several applications arepresented as well.

The class of processes formed as the aggregation of Ornstein-Uhlenbeck processes has proved useful in modeling time series from a number of areas and includes several interesting special cases. This paper examines the second-order properties of this class. Bounds on the one-step prediction error variance are proved and consistency of the minimum contrast estimation is demonstrated.