We prove Lipschitz continuity for local
minimizers of integral functionals of the Calculus of Variations
in the vectorial case, where the energy density depends explicitly
on the space variables and has general growth with respect to the
gradient. One of the models is
$$
F\left(u
\right)=\int_{\Omega}a(x)[h\left(|Du|\right)]^{p(x)}{\rm d}x
$$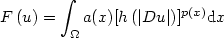 with h a convex function with general growth (also exponential behaviour
is allowed).
with h a convex function with general growth (also exponential behaviour
is allowed).