We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We analyse the decay properties of the solution semigroup S(t) generated by the linear integrodifferential equation
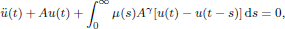
where the operator A is strictly positive self-adjoint with A –1 not necessarily compact. The asymptotic stability of S(t) is investigated in terms of the dependence of the parameter γ ∈ ℝ. In particular, we show that S(t) is not exponentially stable when γ ≠ 1.
