Narrow escape and narrow capture problems which describe the average times required to stop the motion of a randomly travelling particle within a domain have applications in various areas of science. While for general domains, it is known how the escape time decreases with the increase of the trap sizes, for some specific 2D and 3D domains, higher-order asymptotic formulas have been established, providing the dependence of the escape time on the sizes and locations of the traps. Such results allow the use of global optimisation to seek trap arrangements that minimise average escape times. In a recent paper (Iyaniwura (2021) SIAM Rev. 63(3), 525–555), an explicit size- and trap location-dependent expansion of the average mean first passage time (MFPT) in a 2D elliptic domain was derived. The goal of this work is to systematically seek global minima of MFPT for 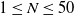$1\leq N\leq 50$ traps in elliptic domains using global optimisation techniques and compare the corresponding putative optimal trap arrangements for different values of the domain eccentricity. Further, an asymptotic formula for the average MFPT in elliptic domains with N circular traps of arbitrary sizes is derived, and sample optimal configurations involving non-equal traps are computed.

A hybrid asymptotic-numerical method is developed to approximate the mean first passage time (MFPT) and the splitting probability for a Brownian particle in a bounded two-dimensional (2D) domain that contains absorbing disks, referred to as “traps”, of asymptotically small radii. In contrast to previous studies that required traps to be spatially well separated, we show how to readily incorporate the effect of a cluster of closely spaced traps by adapting a recently formulated least-squares approach in order to numerically solve certain local problems for the Laplacian near the cluster. We also provide new asymptotic formulae for the MFPT in 2D spatially periodic domains where a trap cluster is centred at the lattice points of an oblique Bravais lattice. Over all such lattices with fixed area for the primitive cell, and for each specific trap set, the average MFPT is smallest for a hexagonal lattice of traps.