1 results
Asymptotic Probabilities of an Exceedance Over Renewal Thresholds with an Application to Risk Theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 153-162
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
-
Let (Yn, Nn)n≥1 be independent and identically distributed bivariate random variables such that the Nn are positive with finite mean ν and the Yn have a common heavy-tailed distribution F. We consider the process (Zn)n≥1 defined by Zn = Yn - Σn-1, where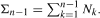
It is shown that the probability that the maximum M = maxn≥1Zn exceeds x is approximately 
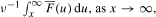as x → ∞, where F' := 1 - F. Then we study the integrated tail of the maximum of a random walk with long-tailed increments and negative drift over the interval [0, σ], defined by some stopping time σ, in the case in which the randomly stopped sum is negative. Finally, an application to risk theory is considered.
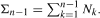It is shown that the probability that the maximum 
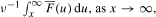as 