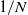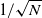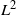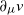The stochastic dynamics of chemical reactions can be accurately described by chemicalmaster equations. An approximated time-evolution equation of the Langevin type has beenproposed by Gillespie based on two explicit dynamical conditions. However, whennumerically solve these chemical Langevin equations, we often have a small stopping time–atime point of having an unphysical solution–in the case of low molecular numbers. Thispaper proposes an approach to simulate stochasticities in chemical reactions withdeterministic delay differential equations. We introduce a deterministic Brownian motiondescribed by delay differential equations, and replace the Gaussian noise in the chemicalLangevin equations by the solutions of these deterministic equations. This modificationcan largely increase the stopping time in simulations and regain the accuracy as in thechemical Langevin equations. The novel aspect of the present study is to apply thedeterministic Brownian motion to chemical reactions. It suggests a possible direction ofdeveloping a hybrid method of simulating dynamic behaviours of complex gene regulationnetworks.