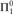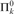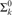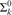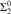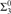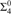1 results
COMPLEXITY OF EQUIVALENCE RELATIONS AND PREORDERS FROM COMPUTABILITY THEORY
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 18 August 2014, pp. 859-881
- Print publication:
- September 2014
-
- Article
- Export citation
-
We study the relative complexity of equivalence relations and preorders from computability theory and complexity theory. Given binary relations R, S, a componentwise reducibility is defined by
R ≤ S ⇔ ∃f ∀x, y [x R y ↔ f (x) S f (y)].
Here, f is taken from a suitable class of effective functions. For us the relations will be on natural numbers, and f must be computable. We show that there is a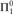
${\rm{\Pi }}_1^0$-complete equivalence relation, but no 
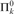${\rm{\Pi }}_k^0$-complete for k ≥ 2. We show that 
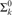${\rm{\Sigma }}_k^0$ preorders arising naturally in the above-mentioned areas are 
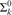${\rm{\Sigma }}_k^0$-complete. This includes polynomial time m-reducibility on exponential time sets, which is 
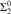${\rm{\Sigma }}_2^0$, almost inclusion on r.e. sets, which is 
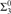${\rm{\Sigma }}_3^0$, and Turing reducibility on r.e. sets, which is 
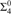${\rm{\Sigma }}_4^0$.
