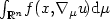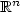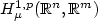Lower semicontinuity results are obtained for multiple
integrals of the kind $\int _{\mathbb{R}^n}\!f(x, \!\nabla_\mu u\!){\rm d} \mu$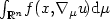 ,
where μ is a given positive measure on $\mathbb{R}^n$
,
where μ is a given positive measure on $\mathbb{R}^n$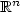 , and the
vector-valued function u belongs to the Sobolev space $H
^{1,p}_\mu (\mathbb{R}^n, \mathbb{R}^m)$
, and the
vector-valued function u belongs to the Sobolev space $H
^{1,p}_\mu (\mathbb{R}^n, \mathbb{R}^m)$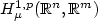 associated with μ. The proofs are
essentially based on blow-up techniques, and a significant role is
played therein by the concepts of tangent space and of tangent
measures to μ. More precisely, for fully general μ, a
notion of quasiconvexity for f along the tangent bundle to
μ, turns out to be necessary for lower semicontinuity; the
sufficiency of such condition is also shown, when μ belongs to
a suitable class of rectifiable measures.
associated with μ. The proofs are
essentially based on blow-up techniques, and a significant role is
played therein by the concepts of tangent space and of tangent
measures to μ. More precisely, for fully general μ, a
notion of quasiconvexity for f along the tangent bundle to
μ, turns out to be necessary for lower semicontinuity; the
sufficiency of such condition is also shown, when μ belongs to
a suitable class of rectifiable measures.