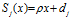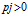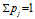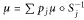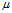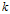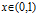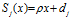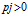Consider a finite sequence of linear contractions ${{S}_{j}}(x)\,=\,\rho x\,+{{d}_{j}}$ and probabilities $pj\,>\,0$ with 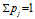$\Sigma \,{{p}_{j}}\,=\,1$. We are interested in the self-similar measure 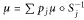$\mu \,=\,\Sigma \,{{p}_{j}}\,\mu \,{}^\circ \,s_{j}^{-1}$, of finite type. In this paper we study the multi-fractal analysis of such measures, extending the theory to measures arising from non-regular probabilities and whose support is not necessarily an interval.

Under some mild technical assumptions, we prove that there exists a subset of supp 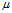$\mu $ of full 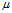$\mu $ and Hausdorff measure, called the truly essential class, for which the set of (upper or lower) local dimensions is a closed interval. Within the truly essential class we show that there exists a point with local dimension exactly equal to the dimension of the support. We give an example where the set of local dimensions is a two element set, with all the elements of the truly essential class giving the same local dimension. We give general criteria for these measures to be absolutely continuous with respect to the associated Hausdorff measure of their support, and we show that the dimension of the support can be computed using only information about the essential class.

To conclude, we present a detailed study of three examples. First, we show that the set of local dimensions of the biased Bernoulli convolution with contraction ratio the inverse of a simple Pisot number always admits an isolated point. We give a precise description of the essential class of a generalized Cantor set of finite type, and show that the 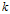$k$-th convolution of the associated Cantor measure has local dimension at 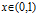$x\,\in \,(0,\,1)$ tending to 1 as 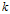$k$ tends to infinity. Lastly, we show that within a maximal loop class that is not truly essential, the set of upper local dimensions need not be an interval. This is in contrast to the case for finite type measures with regular probabilities and full interval support.

Start with a compact set K ⊂ Rd. This has a random number of daughter sets, each of which is a (rotated and scaled) copy of K and all of which are inside K. The random mechanism for producing daughter sets is used independently on each of the daughter sets to produce the second generation of sets, and so on, repeatedly. The random fractal set F is the limit, as n goes to ∞, of the union of the nth generation sets. In addition, K has a (suitable, random) mass which is divided randomly between the daughter sets, and this random division of mass is also repeated independently, indefinitely. This division of mass will correspond to a random self-similar measure on F. The multifractal spectrum of this measure is studied here. Our main contributions are dealing with the geometry of realisations in Rd and drawing systematically on known results for general branching processes. In this way we generalise considerably the results of Arbeiter and Patzschke (1996) and Patzschke (1997).

We consider random recursive fractals and prove fine results about their local behaviour. We show that for a class of random recursive fractals the usual multifractal spectrum is trivial in that all points have the same local dimension. However, by examining the local behaviour of the measure at typical points in the set, we establish the size of fine fluctuations in the measure. The results are proved using a large deviation principle for a class of general branching processes which extends the known large deviation estimates for the supercritical Galton-Watson process.