We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For
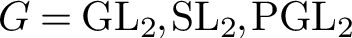$G = \mathrm {GL}_2, \mathrm {SL}_2, \mathrm {PGL}_2$
we compute the intersection E-polynomials and the intersection Poincaré polynomials of the G-character variety of a compact Riemann surface C and of the moduli space of G-Higgs bundles on C of degree zero. We derive several results concerning the P=W conjectures for these singular moduli spaces.
