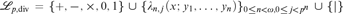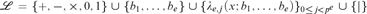1 results
SEPARABLY CLOSED VALUED FIELDS: QUANTIFIER ELIMINATION
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 12 August 2016, pp. 887-900
- Print publication:
- September 2016
-
- Article
- Export citation
-
It is proved in this article that the theory of separably closed nontrivially valued fields of characteristic p > 0 and imperfection degree e > 0 (e ≤ ∞) has quantifier elimination in the language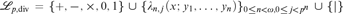
${{\cal L}_{p,{\rm{div}}}} = \{ + , - , \times ,0,1\} \cup {\{ {\lambda _{n,j}}(x;{y_1}, \ldots ,{y_n})\} _{0 \le n < \omega ,0 \le j < {p^n}}} \cup \{ |\}$; in particular, when e is finite, the corresponding theory has quantifier elimination in the language 
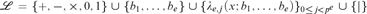${\cal L} = \{ + , - , \times ,0,1\} \cup \{ {b_1}, \ldots ,{b_e}\} \cup {\{ {\lambda _{e,j}}(x;{b_1}, \ldots ,{b_e})\} _{0 \le j < {p^e}}} \cup \{ |\}$.
