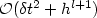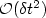We present in this paper the formal passage from a kinetic model to the incompressible Navier−Stokes equations for a mixture of monoatomic gases with different masses. The starting point of this derivation is the collection of coupled Boltzmann equations for the mixture of gases. The diffusion coefficients for the concentrations of the species, as well as the ones appearing in the equations for velocity and temperature, are explicitly computed under the Maxwell molecule assumption in terms of the cross sections appearing at the kinetic level.

The Navier–Stokes equations are approximated by means ofa fractional step, Chorin–Temam projection method; the time derivativeis approximated by a three-level backward finite difference, whereasthe approximation in space is performed by a Galerkin technique.It is shown that the proposed scheme yields an errorof ${\cal O}(\delta t^2 + h^{l+1})$ 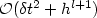for the velocity in the norm of l 2(L2(Ω)d), where l ≥ 1 isthe polynomial degree of the velocity approximation. It is also shownthat the splitting error of projection schemes based on theincremental pressure correction is of ${\cal O}(\delta t^2)$ 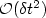independent of theapproximation order of the velocity time derivative.