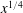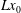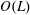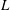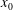In January 2017, a business jet flew in Norway on a short repositioning flight with two pilots onboard, no passengers or cargo. Initially, the take-off proceeded as normal but as the landing gear was retracted both pilots observed that the airspeed was rapidly approaching the flap limiting speed of 200kts. When the flaps were fully retracted at a height of approximately 2,100ft above ground level, the crew experienced a violent nose-down pitch motion. Control was regained at a height of approximately 170ft above ground level and, following the accident, data from the flight data recorder showed that the aircraft experienced –2.62G during the pitch upset. A tailplane stall due to icing was suspected; however, the flight data recorder, being limited to 36 parameters, was not able to confirm this. For expediency during the accident investigation process, a simplified, linear flight dynamics model was developed using Matlab/Simulink to assess static and dynamic stability for a range of tailplane efficiency factors to simulate the effects of tailplane icing.

With the aviation industry facing increasing environmental and energy challenges, there has been a growing demand for sustainable aviation fuel (SAF). Previous studies have shown the role of ice accretion, release and blockage in aviation-related incidents and accidents with conventional jet fuel. However, there is no available data that establishes the magnitude of influence new fuel compositions will pose on ice formation and accretion in aircraft fuel systems. A recirculating fuel test rig capable of cooling fuel from ambient to −30°C within 4h was built by Airbus to simulate conditions in an aircraft wing tank and allow characterisation of ice accretion. The key characteristic was the pressure drop across an inline fuel strainer for the different SAF explored but visual analysis of ice accretion on the strainer mesh (filters used in protecting fuel feed pumps) was also performed for individual experimental runs for comparison. Measurements revealed that 100% conventional fuel exhibited a higher propensity to strainer blockage compared to the SAF tested. However, all SAF blends behaved differently as the blending ratio with Jet A-1 fuel had an impact on the pressure differential at different temperatures. Data from this work are essential to establish confidence in the safe operation of future aircraft fuel systems that will potentially be compatible with 100 % SAF.

The freezing of a water rivulet begins with a water thread flowing over a very cold surface, is naturally followed by the growth of an ice layer and ends up with a water rivulet flowing on a static thin ice wall. The structure of this final ice layer presents a surprising linear shape that thickens with the distance. This paper presents a theoretical model and experimental characterisation of the ice growth dynamics, the final ice shape and the temperature fields. In a first part, we establish a two-dimensional model, based on the advection–diffusion heat equations, that allows us to predict the shape of the ice structure and the temperature fields in both the water and the ice. Then, we study experimentally the formation of the ice layer and we show that both the transient dynamics and the final shape are well captured by the model. In a last part, we characterise experimentally the temperature fields in the ice and in the water, using an infrared camera. The model shows an excellent agreement with the experimental fields. In particular, it predicts well the linear decrease of the water surface temperature observed along the plane, confirming that the final ice shape is a consequence of the interaction between the thermal boundary layer and the free surface.

Icing on aircraft can drastically reduce aerodynamic performance and lead to serious accidents. Therefore, prediction of the accreted ice shape and area and its effects on aerodynamic performance is crucial during the design phase of an aircraft. However, numerical simulations based on conventional grid-based methods such as the finite volume method cannot accurately reproduce the complex ice shapes, which involve horn growth, feather growth, air voids, and severe surface roughness. In the present study, instead of the grid-based method, a hybrid grid- and particle-based method was newly proposed and applied to the icing problem on a NACA0012 airfoil. The explicit moving particle semi-implicit method was employed as the particle-based method due to its short computing time. The numerical simulations effectively reproduced feather-shaped ice, air voids, and surface roughness. Finally, by computing the flow around the iced airfoil, it was confirmed that flow separation around the leading edge occurred due to the ice layer, which resulted in a thicker boundary layer and wake and an increase in the drag coefficient of approximately 70% after a residence time of only 60 seconds.

Water droplet freezing affects many aspects of our daily lives, although there is no comprehensive model which retrieves all of the experimentally observed features when a liquid water droplet deposited on a cold substrate turns to ice. In this paper, we present general governing equations to describe water droplet freezing on a solid substrate by accounting for the physical properties of each phase present, namely the liquid and ice, in addition to the solid substrate. The approach, which takes advantage of the full mean curvature expression of both the droplet–air and liquid–ice interfaces, disjoining pressure, the Gibbs–Thomson effect, natural convection and the substrate thermal and physico-chemical properties, enables us to model a more realistic frozen droplet shape, without a prior assumption for the freezing growth angle. In addition to correctly predicting the freezing time, we capture both qualitatively and quantitatively the key experimentally observed features during water droplet freezing such as volume expansion, concave ice front and the cusp singularity. Furthermore, the proposed equation for the tip angle seems to explain its experimentally observed variability.

In the 1480s, da Vinci invented the first hygrometer using cellulose fibres to attract moisture from the atmosphere. Five hundred years later, Williams and Blanc showed that the depressed vapour pressure of a hygroscopic sessile droplet can inhibit condensation within an annular dry zone on the surface. What remains unresolved to this day is whether these regions of suppressed condensation around hygroscopic agents are due to inhibited nucleation versus inhibited growth of the condensate. We elucidate the competition between these two mechanisms by generating steady-state dry zones about frozen water droplets. The choice of ice as the hygroscopic material was motivated by its unique ability to remain undiluted as it attracts moisture from the air. Experiments, scaling models, and simulations where the ice droplet size, ambient humidity and surface temperature are systematically varied reveal that over the vast majority of the parameter space, the inhibited growth dry zone wins the duel over the nucleation dry zone.

The present study is devoted to the experimental investigation and theoretical modelling of the interaction between fluid flow and solidification during the impact of supercooled water drops onto an ice surface. Using a high-speed video system, the impact process is captured with a high spatial and temporal resolution in a side view. The lamella thinning and the residual ice layer thickness in the centre of impact are determined from the high-speed videos for varying drop and surface temperatures, and impact velocities. It is shown that the temperature of the impact surface has a negligible influence and the drop temperature has a dominating influence on the lamella thinning and the final ice layer thickness. For decreasing drop temperatures, higher freezing rates cause a decreased rate of lamella thinning and a larger thickness of the resulting ice layer. On the other hand, a higher impact velocity causes an increasing speed of lamella thinning and a smaller thickness of the resulting ice layer. Based on a postulated flow in the spreading lamella and considering the ice layer growth and the developing viscous boundary layer, the upper limit for the resulting ice layer thickness is theoretically modelled. The theory shows very good agreement with the experimental results for all impact conditions. Based on the derived theoretical scaling, a semi-empirical equation is obtained which allows an a priori prediction of the final ice layer thickness resulting from a single drop impact, knowing the impact conditions. This capability is important for the improvement of existing ice accretion models.

We present a model for ice formation in a thin, viscous liquid film driven by a Blasius boundary layer after heating is switched off along part of the flat plate. The flow is assumed to initially be in the Nelson et al. (J. Fluid Mech., vol. 284, 1995, pp. 159–169) steady-state configuration with a constant flux of liquid supplied at the tip of the plate, so that the film thickness grows like 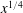$x^{1/4}$ in distance along the plate. Plate cooling is applied downstream of a point, 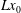$Lx_{0}$, an 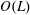$O(L)$-distance from the tip of the plate, where 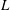$L$ is much larger than the film thickness. The cooling is assumed to be slow enough that the flow is quasi-steady. We present a thorough asymptotic derivation of the governing equations from the incompressible Navier–Stokes equations in each fluid and the corresponding Stefan problem for ice growth. The problem breaks down into two temporal regimes corresponding to the relative size of the temperature difference across the ice, which are analysed in detail asymptotically and numerically. In each regime, two distinct spatial regions arise, an outer region of the length scale of the plate, and an inner region close to 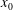$x_{0}$ in which the film and air are driven over the growing ice layer. Moreover, in the early time regime, there is an additional intermediate region in which the air–water interface propagates a slope discontinuity downstream due to the sudden onset of the ice at the switch-off point. For each regime, we present ice profiles and growth rates, and show that for large times, the film is predicted to rupture in the outer region when the slope discontinuity becomes sufficiently enhanced.