We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We obtain sharp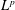 
$L^{p}$ bounds for oscillatory integral operators with generic homogeneous polynomial phases in several variables. The phases considered in this paper satisfy the rank one condition that is an important notion introduced by Greenleaf, Pramanik, and Tang. Under certain additional assumptions, we can establish sharp damping estimates with critical exponents to prove endpoint 
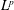$L^{p}$ estimates.
