1 results
UNIVERSAL MINIMAL FLOWS OF GENERALIZED WAŻEWSKI DENDRITES
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1618-1632
- Print publication:
- December 2018
-
- Article
- Export citation
-
We study universal minimal flows of the homeomorphism groups of generalized Ważewski dendrites WP,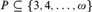
$P \subseteq \left\{ {3,4, \ldots ,\omega } \right\}$. If P is finite, we prove that the universal minimal flow of the homeomorphism group H (WP) is metrizable and we compute it explicitly. This answers a question of Duchesne. If P is infinite, we show that the universal minimal flow of H (WP) is not metrizable. This provides examples of topological groups which are Roelcke precompact and have a nonmetrizable universal minimal flow with a comeager orbit.
