Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (1)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

heteroclinic intersection

Journal of the Institute of Mathematics of Jussieu (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

CENTER MANIFOLDS FOR PARTIALLY HYPERBOLIC SETS WITHOUT STRONG UNSTABLE CONNECTIONS
Part of
- Smooth dynamical systems: general theory
- Dynamical systems with hyperbolic behavior
Christian Bonatti, Sylvain Crovisier
Journal:

Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016

Published online by Cambridge University Press:

11 March 2015, pp. 785-828

Print publication:

October 2016
- Article
- - You have access
- PDF
- Export citation
We consider compact sets which are invariant and partially hyperbolic under the dynamics of a diffeomorphism of a manifold. We prove that such a set 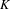$K$ is contained in a locally invariant center submanifold if and only if each strong stable and strong unstable leaf intersects $K$ at exactly one point.