In this paper we show that a polynomial equation admits infinitely many prime-tuple solutions, assuming only that the equation satisfies suitable local conditions and the polynomial is sufficiently non-degenerate algebraically. Our notion of algebraic non-degeneracy is related to the 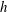 $h$-invariant introduced by W. M. Schmidt. Our results prove a conjecture by B. Cook and Á. Magyar for hypersurfaces of degree 3.
$h$-invariant introduced by W. M. Schmidt. Our results prove a conjecture by B. Cook and Á. Magyar for hypersurfaces of degree 3.
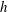 $h$-invariant
$h$-invariant