In this paper we study the group K2n(n+1)(F) where F is the function field of a complete, smooth, geometrically irreducible curve C over a number field, assuming the Beilinson–Soulé conjecture on weights. In particular, we compute the Beilinson regulator on a subgroup of K2n(n+1)(F), using the complexes constructed in Compositio Math. 96 (1995), pp. 197–247. We study the boundary map in the localization sequence for n=2 and n=3. We combine our results with results of Goncharov in order to obtain a complete description of the image of the regulator map on K4(3)(C) and K6(4)(C) (which have the same images as K4(C)$⊗ _{\Bbb Z}\, {\Bbb Q}$, and K6(C)$⊗ _{\Bbb Z}\, {\Bbb Q}$, respectively), independent of any conjectures.
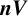 $\boldsymbol {nV}$
$\boldsymbol {nV}$