We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study a fractional-order delayed predator-prey model with Holling–Tanner-type functional response. Mainly, by choosing the delay time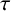 
$\tau $
as the bifurcation parameter, we show that Hopf bifurcation can occur as the delay time 
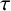$\tau $
passes some critical values. The local stability of a positive equilibrium and the existence of the Hopf bifurcations are established, and numerical simulations for justifying the theoretical analysis are also presented.
