We investigate the supports of extremal martingale measures with prespecified marginals in a two-period setting. First, we establish in full generality the equivalence between the extremality of a given measure Q and the denseness in 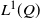$L^1(Q)$ of a suitable linear subspace, which can be seen in a financial context as the set of all semistatic trading strategies. Moreover, when the supports of both marginals are countable, we focus on the slightly stronger notion of weak exact predictable representation property (WEP) and provide two combinatorial sufficient conditions, called the ‘2-link property’ and ‘full erasability’, on how the points in the supports are linked to each other for granting extremality. When the support of the first marginal is a finite set, we give a necessary and sufficient condition for the WEP to hold in terms of the new concepts of 2-net and deadlock. Finally, we study the relation between cycles and extremality.